Reverse Engineering Code Art - Part 6 - Noisy Donuts

Based on this dwitter by Pascal

c.width=w=70;for(i=2800;i--;)x.fillRect(X=i%w,Y=(i-X)/w,0<T(T(S(X/7+5*C(t))+S(Y/7-5*t))),1)

---

Format & Analysis

The code is simple, there is a lot of math to explain

const u = (t) => {
  c.width = w = 70;
  for (i = 2800; i--; ) {
    const X = i % w;
    const Y = (i - X) / w;
    const angle = S(X / 7 + 5 * t) + S(Y / 7 - 5 * t) 
    const val = T(T(angle));
    x.fillRect(X, Y, 0 < val, 1);
  }
};

I’m making a small change to make things easier to understand, isolating the moving effect to one direction by changing S(X / 7 + 5 * C(t)) to S(X / 7 + 5 * t)

Our main focus is around two functions

sin(x) + sin(x)

This is rather a simple function

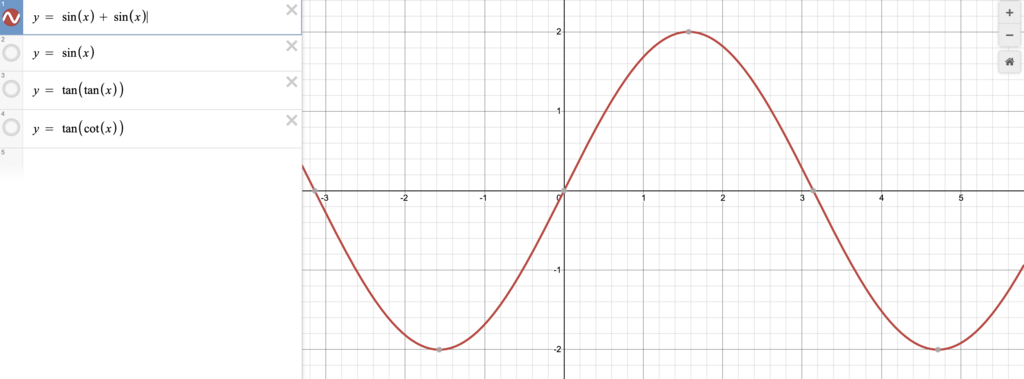
We can visualizing it by

x.fillRect(X, Y, S(X / 7 + 5 * t) + S(Y / 7 - 5 * t), 1)

It’s seeing the 2D graph in a 1D pixel space

Another example dwitter, but with sin(x) + cos(x)

tan(tan(x))

The function y = tan(tan(x)) has multiple bands.

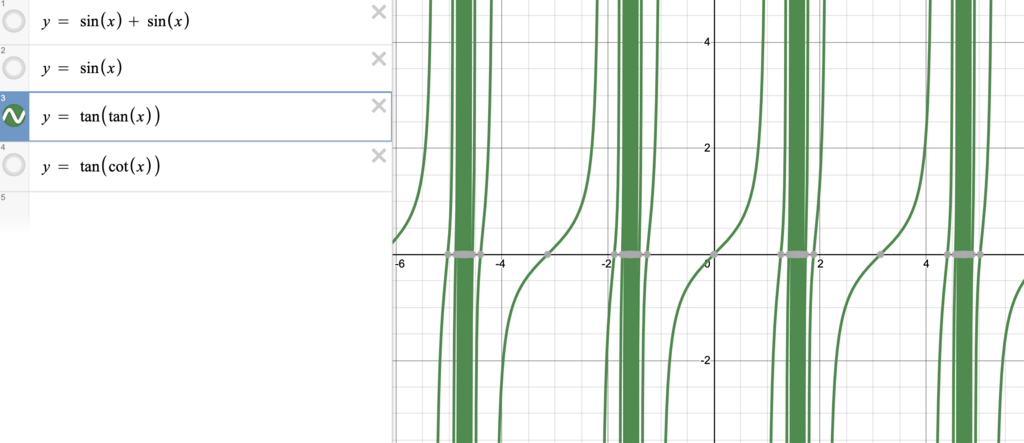
In each band these are infinitely transitions from Inf to -Inf, this causes the noise effect that we see

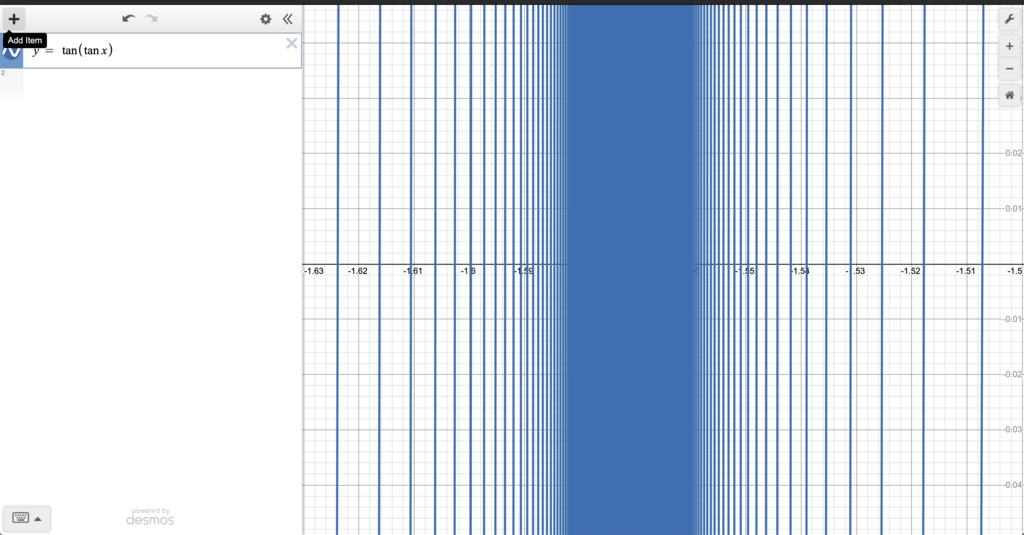
The below is the function from x -1.6 to -1.5

By adding the factor of time the noise circles behave chaotically